What is a Monoid?
Monoid is a property of a system which satisfies these three laws:
- Has identity
- Is composable and the order of composition doesnot matter: i.e. composition is associative
- The result of composing 2 such system produces similar system. i.e Closure property or endomorphism.
Well, that sounds a bit abstract. Indeed. Well, is this any useful in programming? You bet it is.
This post is entirely about understanding what a monoid is, with ideas we (OOP) programmers already know. To do so, I will do a addition on data models (bill) and then discuss the flaws, our imperative system has. And then, we will see how monoids naturally come to our rescue.
One thing you need to have in mind as we go is that all we are trying to do is composability of smaller functions to build something useful.
Monoid is not a direct relative of Monad. It is not a semi-monad or a smaller form of Monad. Its a separate concept that has not much to do with Monad
Lets establish a mental picture of monoid now!
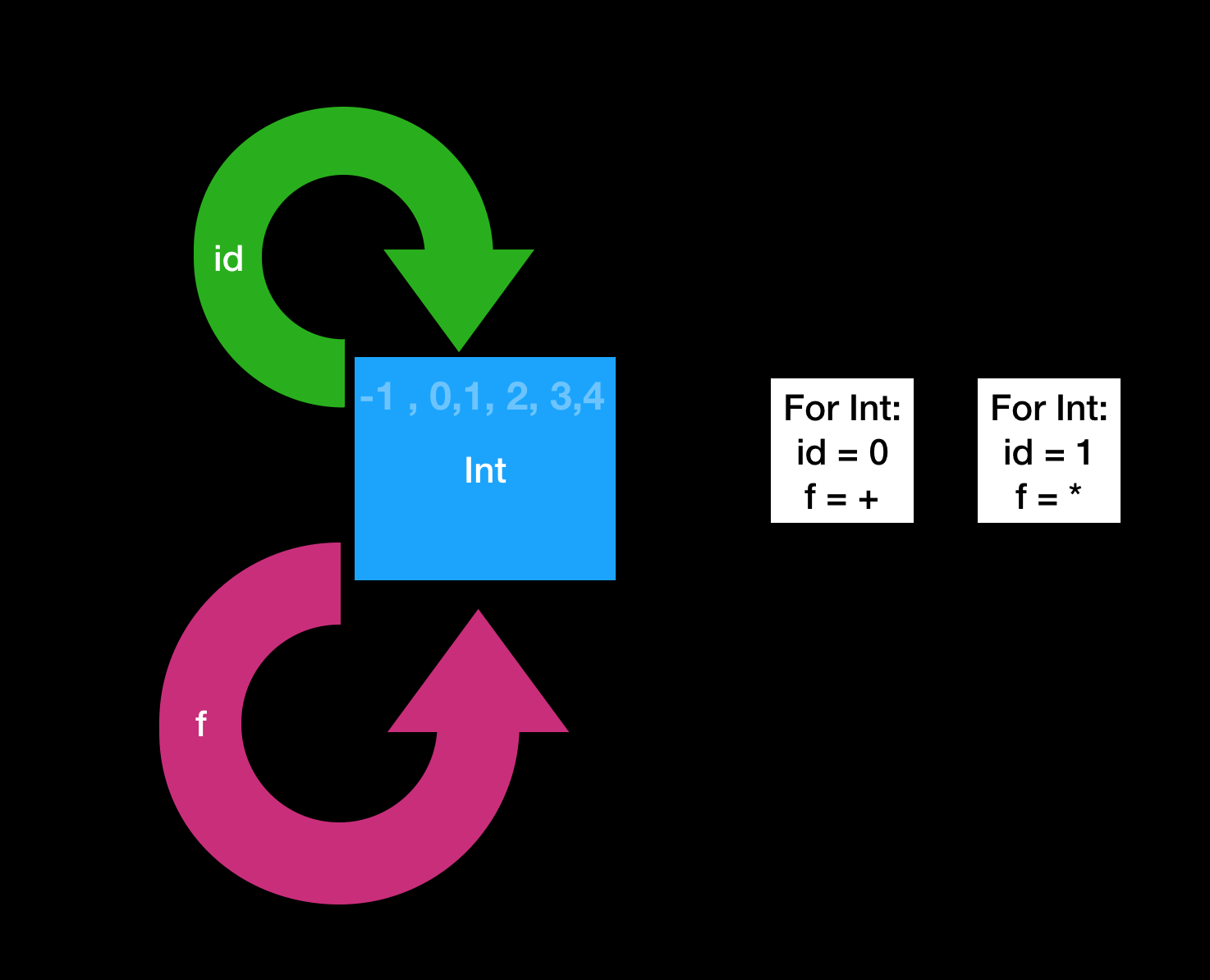
-
Lets represnt
Inttype as a Set/Box of raw numbers. -
idis the identity function. -
fis the function that will compose 1 or more values ofInttype. Functoionfhas to return anotherIntvlaue to satisfy the closure property. -
Lets try to prove Int is
monoid in addition (+).+is a operator function.any number + id = any numbersoid= 0fis the+operator. Its signature statisfies that the output is also a value in typeInt
func +(_ lhs: Int, _ rhs: Int) -> Int {...} -
Thus,
Intis a monoid in terms of+operation. You could do the same withIntin terms of*but not-.
With that picture in mind, let move on!
Problem
Let say we are making a POS(Point Of Sale) application where given a bunch of BillReceipts we need to calculate and print the total amount. Jack happens to be our loyal frequent customer.
Lets assume the data model for the BillReceipt is as follows:
struct BillReceipt {
let name: String
let quantity: Int
let totalPrice: Double
}
And here we have a list of items Jack ordered.
let mangoBill = BillReceipt(name: "Mango", quantity: 2, totalPrice: 1.5)
let orangeBill = BillReceipt(name: "Orange", quantity: 3, totalPrice: 2)
let spagettiBill = BillReceipt(name: "Spagetti", quantity: 1, totalPrice: 2.1)
// then
let allReceipts = [mangoBill, orangeBill, spagettiBill]
Now we need to total them up and ask for money. Fair and easy. Lets do this.
We will now go through couple of ways one might tackle this problem. However, our aim is to eventually refine to and try to reach a monoidal approach. Lets get going.
1. Imperative (Von Neumann’s Word at a time processing)
func total(_ bills: [BillReceipt]) {
var totalPrice = 0.0
var totalQuantity = 0
for index in allReceipts {
// Picking each element:: Von Neumann's Word at Time processing
totalPrice += index.totalPrice
totalQuantity += index.quantity
}
print("Impure Totaling Fucntion:")
print("Total")
print("Quantity \t\t",totalQuantity)
print("Total Price \t", totalPrice)
print("\n")
}
Disucssion:
- Whats good?
- Its very simple.
- Whats not good?
- Lets say we processed Jacks total. But wait, lets say Jack quickly runs to get some bananas (Unlike most of us, he has the last minute recalling what he forgot to grab from the market). We would have to add bananaReceipt to the allBills list and compute everything over again. We can’t just add only bananasReceipt to the total we obtained earlier.
- The code is picking a receipt and mutating the accumulators. This is item at a time processing. Lets redo this atleast with nice functional programming skills under our belt.
2. Functional (Declarative)
let total = allReceipts.reduce((0.0, 0)) { ($0.0 + $1.totalPrice, $0.1 + $1.quantity) }
// Printing is left out intentionally
Discussion:
-
Whats good?
- Its quite simple.
- We are declarative. We are now not concerned about each element in the list. This is what it means to get rid of Word at time processing.
- concise code.
-
Whats not so good?
- Not much besides the arbitary initial value tuple
(0.0, 0). - We need to update the initial value tuple when later on we change the information we want to extract from the Receipt.
- More importantly, we haven’t quite dealt with how we could address Jack’s problem to buying more stuff after we processed his bills. Jack goes to buy bananas on last minute here too. Here’s how we might solve it.
let bananaBill = BillReceipt(...) let totalYetAgain = (total.0 + bananaBill.price, total.1 + bananaBill.quantity)- Does this look Ad-hoc hack to support incremental addition. Lets see what Monoid has to offer.
\
- Not much besides the arbitary initial value tuple
3. Monoidal Addition:
//1.
extension BillReceipt {
static func add(_ first: BillReceipt, _ second: BillReceipt) -> BillReceipt {
let addedPrice = first.totalPrice + second.totalPrice
let addedQuantity = first.quantity + second.quantity
let addedName = "Total"
return BillReceipt(name: addedName, quantity: addedQuantity, totalPrice: addedPrice)
}
}
//2.
let totalPureMonoidal = allReceipts.reduce(WHATDOIPUTHERE, BillReceipt.add)
Here, we defined a add as type function that takes two BillRecipts and returns added result in a BillReceipt. This is the First Law of Monoid called Closure Property.
- i.e
add :: BillReceipt -> BillReceipt -> BillReceipton curried notation. - similar to
add:: Int -> Int -> Intforadd(Int, Int) -> Int - Note that for closure property; return type must match the input argument type
Nice!!! (It really doesnot matter if this is a instance or type function. I chosed type function because its easy to plug into list.reduce. See point 2 above)
Make note of WHATDOIPUTHERE up in the code. So what is the initial value? Lets take a moment and do addtion on Ints and String.
let sum = [1,2,3,4].reduce(0, +)
let product = [1,2,3,4].reduce(1, *)
let joinedString = ["Hello", " ", " there ", "^-^"].reduce("", +)
// Keep an eye on this one too
[1,2,3,4].reduce(0, -)
All of this above methods have a clear defined inital values.
- In case of
Int +we have0. i.e.x + 0 = xor0 + x = x - In case of
Int *we have1. i.e.x * 1 = x - In case of
String +we have"". i.estring + "" = string
From the above observation, Its obvious that the initial Value for reduce is more likely the identity for Types operation. Now the question is, what is the identity for our BillReceipt type’s add() function?
Searching for BillReceipt Identity
So lets default all the values of member to their identity and hope we will find one.
extension BillReceipt {
init() {
name = ""
quantity = 0
totalPrice = 0
}
}
- Please note that, I extended Struct and added init() so that I will also get the default memberwise initializer that structs gives us for free. I now have both initializer. If you implement this
init()inside the Struct then the memberwise initializer is not provided
So here we are:
let totalPureMonoidal = allReceipts.reduce(BillReceipt(), BillReceipt.add)
Disucssion:
-
Whats good?
- Still everything is simple.
- We factored out additon logic to a small function.
- We saw
Closure propertyandIndentityforBillReceipt's add() operation - If Jack goes to buy banans late, as he always does, then we can incrementally add his banana receipt without any hack.
let totalWithLastMinuteBananas = BillReceipt.add(totoalPureMonoidal, bananaReceipt) -
Whats not good?
- We have yet to see the
Associativitylaw. - We are ignoring the
nameproperty ofBillReceiptwhile doing theadd()operation. What if BillReceipt were to have more fields likepricePerItem: Double. What do we do when we add 2 such structs?
- We have yet to see the
extension BillReceipt {
static func add(_ first: BillReceipt, _ second: BillReceipt) -> BillReceipt {
let addedPrice = first.totalPrice + second.totalPrice
let addedQuantity = first.quantity + second.quantity
let addedName = "Total"
let addedPricePerItem = ...... //WATTTT TO DO HERE
return BillReceipt(name: addedName, quantity: addedQuantity, totalPrice: addedPrice)
}
}
Associativity
First off, lets get this associativity right.
These are associative as the order of operation application doesnot matter.
(1 + 2) + 3 == 1 + (2 + 3)
(4 * 5) * 7 == 4 * (5 * 7)
("Hello " + "there") + "Monoid" == "Hello " + ("there" + "Monoid")
However, substraction satisfied identity and closure property but it doesnot hold true for associativity.
(1 - 2) - 3 != 1 - (2 - 3)
Thus, from the laws for monoid.
- Addition on Int/Double is Monoid
- Multiplication on Int/Double is Monoid
- String concatnation is Monoid.
However,
- Substraction on Int/Double is not Monoid as it is not associative.
- Similar for Division.
What about add on BillReceipt?
-
It fulfills closure property.
// When we apply .add() the result is same type as the input type BillReceipt.add(mangoBill, BillReceipt(name: "Pizza", quantity: 3, totalPrice: 9.5)) is BillReceipt -
It fulfills associativite property.
// This allows our reduce function to be parallelized if necessary let addedLeft = BillReceipt.add(BillReceipt.add(mangoBill, orangeBill), spagettiBill) let addedRight = BillReceipt.add(mangoBill, BillReceipt.add(orangeBill, spagettiBill)) addedLeft == addedRight // similar to (1 + 2) + 3 == 1 + (2 + 3) -
It has a proper identity.
BillReceipt.add(mangoBill, BillReceipt()) == mangoBill // similar to 1 + 0 = 1 BillReceipt.add(BillReceipt(), orangeBill) == orangeBill -
addonBillReceiptis a Monoid.✅💪
Why the fuss? Why the Monoid?
Before going too far, lets appreciate what have we got from Monoids.
Benifits of Associativity
-
Parallelization: Take for instance how Hadoop works?
12 + 10 + 6 + 9 + 100 + 20 + 13 ==> Core1 (12 + 10) | Core2 (6 + 9) | Core3(100 + 20) | Core4 (13) ==> Core1(22 + 15) | Core2(...) | Core3(120 + 13) | Core4(...) ==> Core1(37 + 133) | Core2(...) | Core3(...) | Core4(...) ==> Core1(170) | Core2(...) | Core3(...) | Core4(...) -
Incrementalism: We saw this one before with Jack’s last minute bananas purchase addition.
-
Divide And Conquer: The first point on parallelization is good example of how a compiler might choose to divide and conquer strategy.
-
Composability
Benifits of Closure
-
a pairwise operation (binary operation) can be converted to work on lists and sequences for free.
1 + 2 + 3 + 4 [1,2,3,4].reduce(0, +)
Identity
Identity helps us answer what do we do in these situations:
- How to
reduceon a empty list? What is the initial value of thereduce?
[].reduce(BillReceipt(), BillReceipt.add)
[Int]().reduce(0, +) //sum of empty list of ints is 0
- Provides either a starting data when the list of addition to make is a empty list. Provides terminal data when using divide and conquer algorithms.
Sum it up
Despite the fact that we didn’t saw much of theory behind Monoid and how category theory pictographically describes Monoid, we did create a Monoid for us. The above problem helped us understand that if we end up having a Monoid, we can do list comprehension using reduce for free. We can parallelize and incrementally add operations on to the result.
In the end, if I have one senetence to sum it up: Monoid is a way to describe aggregation pattern. List comprehension using reduce is just a prime example of it.